МЕТОДЫ ПОЛУЧЕНИЯ ДИСКРЕТНЫХ АНАЛОГОВ

 

Дискретизацию дифференциального уравнения можно осуществить множеством способов.

Использование рядов Тейлора. Обычная процедура получения конечно-разностных уравнений заключается в аппроксимации про­изводных в дифференциальном уравнении обрезанными рядами Тейлора.

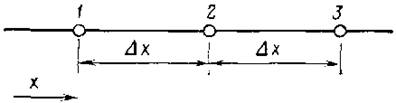
Рис. 2.1. Три последовательные узло­вые точки, используемые при разло­жении в ряд Тэйлора

Рассмотрим узловые точки, показанные на рис. 2.1. Разложение в ряд Тэйлора около узловой точки 2, расположенной посередине между точками 1 и 3 (так что ), дает

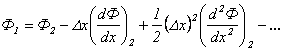;	(2.2)

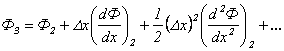;	(2.3)

Отбрасывая члены обоих рядов, начиная с четвертого, вычитая и складывая уравнения, получаем

	(2.4)

и

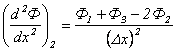.	(2.5)

Подставляя эти выражения в дифференциальное уравнение, можно получить конечно-разностное уравнение.

В данном методе предполагается, что изменение  в зависи­мости от  близко к полиномиальному, так что высшими произ­водными можно пренебречь. Однако это предположение приводит к нежелательным последствиям, например, для случая экспонен­циального изменения . Вывод с помощью рядов Тэйлора сравнительно прост, но менее гибок и не способствует пониманию физического смысла членов урав­нения.

Вариационный метод. Другой метод получения дискретных аналогов основывается на вариационном исчислении.

В вариационном исчислении показано, что решение данных дифференциальных уравнений эквивалентно минимизации соответ­ствующей величины — функционала. Эта эквивалентность назы­вается вариационным принципом. Искомый дискретный аналог по­лучается из условий минимума функционала относительно значе­ний зависимой переменной в узловых точках. Вариационный метод очень часто используется в конечно-элементных методах исследо­вания напряжений, где его можно связать с принципом виртуаль­ных перемещений. Кроме математической сложности и трудности понимания основным недостатком метода является его ограничен­ная применимость, связанная с тем, что вариационный принцип существует не для всех представляющих интерес дифференциаль­ных уравнений.

Метод взвешенных невязок. Эффективным методом решения дифференциальных уравнений является метод взвешенных невязок. Основной подход прост и интересен. Представим дифференциальное уравнение в виде

.	(2.6)

Предположим, что приближенное решение  имеет, например, вид

;	(2.7)

где  — неизвестные параметры. Подставим  в дифференциаль­ное уравнение (2.6) и выделим невязку , которая равна:

.	(2.8)

Мы хотим сделать этот остаток в известном смысле малым. Предположим, что

,	(2.9)

где  — весовая функция, а интеграл берется по рассматриваемой области. Выбирая последовательность весовых функций, можно получить количество уравнений, достаточное для нахождения пара­метров. Решив полученную систему алгебраических уравнений для неизвестных параметров, найдем приближенное решение диффе­ренциального уравнения. Выбирая различные классы весовых функций, можно получить различные версии метода (имеющие свои названия).

Данный метод широко использовался для решения уравнений пограничного слоя, пока его почти не вытеснил метод конечных разностей. Однако можно установить его связь с конечно-разност­ным методом, или, точнее, с методом дискретизации, если рас­сматривать приближенное решение  не в виде единственной для всей области алгебраической функции, а как кусочный профиль с неизвестными параметрами, представляющими собой значе­ния  в узловых точках. Действительно, большая часть недавних разработок метода конечных элементов также основана на при­менении кусочных профилей в сочетании с разновидностью метода взвешенных невязок, известной как метод Галеркина.

Простейшей весовой функцией является . С помощью такой функции можно в рамках данного метода построить систему уравнений, разбивая расчетную область на подобласти или кон­трольные объемы и выбирая в качестве весовых функций, одно­временно равные единице в одной из подобластей и нулю во всех остальных. Этот вариант метода взвешенных невязок называется методом подобласти или методом контрольного объема. В нем полагается, что интеграл от невязки по каждому контрольному объему должен быть равен нулю.

Метод контрольного объема. Часто в элементарных учебниках по теплообмену приводят вывод конечно-разностного уравнения с помощью метода рядов Тэйлора, а затем показывают, что резуль­тирующее уравнение соответствует условию теплового баланса в небольшой области, содержащей узловую точку. Мы также видели, что метод контрольного объема можно рассматривать как частный случай метода взвешенных невязок. Основная идея метода кон­трольного объема легко понятна и поддается прямой физической интерпретации. Расчетную область разбивают на некоторое число непересекающихся контрольных объемов таким образом, что каж­дая узловая точка содержится в одном контрольном объеме. Дифференциальное уравнение интегрируют по каждому контроль­ному объему. Для вычисления интегралов используют кусочные профили, которые описывают изменение  между узловыми точ­ками. В результате находят дискретный аналог дифференциаль­ного уравнения, в который входят значения  в нескольких узловых точках.

Полученный подобным образом дискретный аналог выражает закон сохранения  для конечного контрольного объема точно так же, как дифференциальное уравнение выражает закон сохра­нения для бесконечно малого контрольного объема. Одним из важных свойств метода контрольного объема является то, что в нем заложено точное интегральное сохранение таких величин, как масса, количество движения и энергия на любой группе контроль­ных объемов и, следовательно, на всей расчетной области. Это свойство проявляется при любом числе узловых точек, а не только в предельном случае очень большого их числа. Таким образом, даже решение на грубой сетке удовлетворяет точным интеграль­ным балансам.

Результат решения дискретных уравнений относительно значе­ний в узловых точках можно рассматривать двояко. В методе конечных элементов и большинстве методов взвешенных невязок в качестве приближенного решения берется предполагаемое изме­нение , состоящее из значений в узловых точках и интерполя­ционных функций (или профилей) между узловыми точками. Напротив, в конечно-разностном методе в качестве решения рас­сматриваются только значения  в узловых точках и не делается никаких явных указаний о характере изменения  между этими точками. Эта ситуация напоминает лабораторный эксперимент, в котором распределение величины дается в виде измеренных значений в некоторых дискретных точках и не определяется ее изменение в промежутках между этими точками. Мы также ис­пользуем этот подход в методе контрольного объема и будем искать решение в виде значений только в узловых точках. Интер­поляционные формулы или профили будем рассматривать как вспомогательные, необходимые для расчета интегралов. После по­лучения дискретных аналогов предположения о характере профи­лей можно не учитывать. Такая точка зрения дает полную свободу использования различных профилей для интегрирования разных членов дифференциального уравнения.

Для большей ясности применим метод контрольного объема к простой задаче.

Рассмотрим стационарную одномерную задачу теплопроводности, описывае­мую уравнением

,	(2.10)

где  — коэффициент теплопроводности;  — температура;  — скорость выде­ления теплоты в единице объема.

Подготовка. Для получения дискретного аналога будет использовано пока­занное па рис. 2.2 расположение узловых точек.

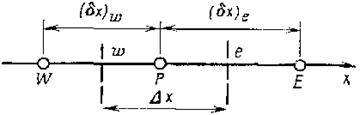
Рис 2.2. Шаблон узловых точек для одномерной задачи

Рис. 2.3. Простые аппроксимации профилей:

а — ступенчатый профиль; б — кусочно-ли­нейный профиль

В центре нашего внимания оказывается точка Р, окруженная точками Е и W (Е— восточная сторона, т. е. направление вдоль оси ; W — западная сторона, т. е. направление, обратное направлению оси ). Штрихом показаны границы  контрольного   объема;   сейчас нас не интересует их точное расположе­ние. Эти границы обозначены буквами е и w. Для рассматриваемой одномер­ной задачи предположим, что размеры контрольного объема в направлениях  и  равны единице.    Таким образом, объем показанного контрольного объема равен . Интегрируя (2.10) по контрольному объему, получаем

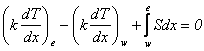.	(2.11)

Предположение о виде профиля. Сделаем теперь предположение о виде профиля или интерполяционной формулы. На рис. 2.3 показаны два простых профиля. В простейшем случае предполагается, что значение  в узловой точке сохраняется для всего окружающего ее контрольного объема. Это предположе­ние приводит к показанному на рис. 2.3,а ступенчатому профилю. Для такого профиля производная  на границах контрольного объема (т. е. в точках w или е) не определена. Эта трудность не возникает для кусочно-линейного профиля (рис. 2.3,6), у которого изменение  между узловыми точками описы­вается линейными интерполяционными функциями.

Дискретный аналог. Использовав для определения  в уравнении (2.11) кусочно-линейный профиль, получим

,	(2.12)

где  — среднее по контрольному объему значение . Полезно записать уравне­ние (2.12) в следующем виде:

,	(2.13)

-где

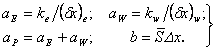
	(2.14)

Необходимо сделать следующие примечания:

1. Уравнение (2.13) записано в стандартном виде. В левой части этого уравнения находится темпе­ратура  в центральной узловой точке, а в правой — температуры в соседних точках и постоянная . В двух- и трехмерном слу­чаях число соседних точек возрастет. В общем случае удобно представить урав­нение (2.13) в виде

,	(2.15)

где индекс  обозначает соседние точки, и суммирование производится по всем соседним точкам.

2. При выводе уравнения (2.13) использовалось простейшее приближение для профиля, позволившее рассчитать . Конечно, возможно применение множества других интерполяционных функций.

3. Важно также понимать, что для различных величин можно использовать разные профили. Например, для вычисления  необязательно предполагать линейный характер изменения  между узловыми точками, так же как необя­зательно рассчитывать  по его линейному изменению от  до .

4. Нет необходимости использовать одинаковые профили для всех членов одного уравнения. Например, если бы в уравнение (2.10) входил дополнитель­ный член, включающий , можно было бы при­менить для его аппроксимации ступенчатый про­филь вместо кусочнолинейного профиля, исполь­зованного для определения .

Основные принципы выбора интерполяцион­ных функций и профилей. Указанная выше сво­бода выбора интерполяционных функций и про­филей ведет к существованию множества спосо­бов получения дискретных аналогов уравнения. Предполагается, что при увеличении числа узло­вых точек решения всех дискретных аналогов ис­ходного уравнения совпадают. Однако наложим дополнительное требование, которое приведет к сужению числа подходящих формул. Потребуем, чтобы решение, полученное даже на грубой сет­ке, во-первых, всегда имело физически правдо­подобный характер и, во-вторых, сохраняло полный баланс.

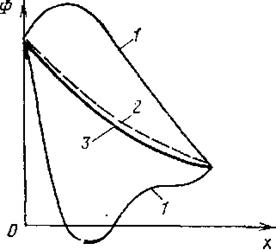
Рис. 2.4. Физически неправ­доподобные (1), правдопо­добное (2) и точное (3) ре­шения

Понять, насколько физично полученное решение, легко, по крайней мере, в простых случаях (рис. 2.4). Правдоподобное решение должно иметь такой же качественный характер, что и точное решение. В задаче теплопроводности без источников никакой профиль температуры не может выходить за пределы тем­ператур границ тела. При охлаждении нагретого твердого тела окружающей его жидкостью температура тела не может стать ниже температуры жидкости.

Условие полного баланса предполагает интегральное сохранение рассматри­ваемой величины во всей расчетной области. Мы будет утверждать, что тепло­вые потоки, массовые расходы и потоки количества движения должны правиль­но отражать баланс с соответствующими источниками и стоками, причем для любого числа узловых точек, а не только в пределе при очень большом числе точек.

Такую возможность сохранения полного баланса дает метод контрольного объема, но при этом необходимо обеспечить, как вскоре увидим, правильный расчет потоков на границах контрольного объема.

Аппроксимация источникового члена. Прежде чем перейти к определению основных правил, рассмотрим источниковый член  уравнения (2.10). Часто источниковый член является функцией самой зависимой переменной , и тогда желательно учесть эту зависимость при построении дискретного аналога. Одна­ко формально можем учитывать только линейную зависимость, так как решение дискретных уравнений будет осуществляться, с помощью методов решения систем линейных алгебраических уравнений. Запишем среднее значение  в виде

,	(2.16)

где  представляет собой постоянную составляющую , a  — коэффициент (очевидно, что  не есть значение  в точке Р).

Наличие  в (2.16) отражает тот факт, что при записи среднего значения  мы предполагали, что значение  распространяется на весь контрольный объем, другими словами, использовался показанный на рис. 3.3,а ступенчатый профиль (следует заметить, что можно использовать ступенчатый профиль для  и кусочно-линейный для члена ).

Дискретный аналог уравнения теплопроводности с линеаризованным источниковым членом будет иметь такой же вид, как и (2.13), но с другими выраже­ниями для коэффициентов:

,	(2.17)

где

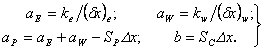
	(2.18)