ОСНОВНЫЕ ПРАВИЛА ПОСТРОЕНИЯ ДИСКРЕТНЫХ АНАЛОГОВ

 

Соответствие потоков на границах контрольного объема. Выражение потока через границу, общую для двух при­легающих контрольных объемов, при записи дискретных аналогов уравнения для этих объемов должно быть одним и тем же.

Обсуждение. Очевидно, что тепловой поток, покидающий один контрольный объем через его границу, должен быть равен потоку, входящему через эту границу в соседний контрольный объем. В противном случае не будет сохраняться полный баланс теплоты. Хотя это требование и легко понять, надо следить, чтобы не было даже небольших его нарушений. Для изображенного на рис. 2.2 контрольного объема можно было рассчитать тепловые потоки  на границе по квадратичному профилю, проходящему через ,  и . При использовании аппроксимации такого же типа для следующего контрольного объема градиент  на общей границе окажется рассчитанным по различным профилям в зави­симости от того, какой из контрольных объемов рассматривается. Получающееся несоответствие  (и, следовательно, тепло­вого потока) показано на рис. 2.5. Для границ, расположенных посередине между узловыми точками тип квадратичного профиля не приводит к какому-либо не­соответствию. Это вызвано тем, что угол наклона касательной к параболе в точке, лежащей посередине между двумя узловыми, в точности равен углу наклона прямой линии, соединяющей значения зависимой переменной в этих точках. Однако это свойство параболы следует рассматривать как случайное, и в общем случае следует избегать изменения выражений на границах между узлами при переходе от одного контрольного объема к другому.

 

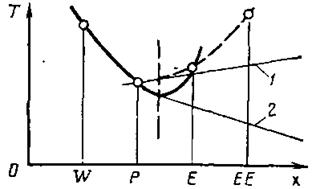
Рис. 2.5. Несоответствие пото­ков, вызванное использованием квадратичного профиля:

1 —касательная к правому про­филю; 2 — касательная к левому профилю

К несоответствию потоков может привести также предположе­ние о том, что все потоки на границах данного контрольного объема описываются с помощью значения коэффициента теплопро­водности в центральной точке . Тогда тепловой поток на гра­нице  (показанной на рис. 2.2) будет выражен через  для окружающего точку  контрольного объема и через  при записи разностного аналога для кон­трольного объема с точкой  в центре. Чтобы избежать таких несоответствий, полезно помнить, что поток на границе рассматривается сам по себе, а не как принадлежащий определенному контрольному объему.

Положительность коэф­фициентов. В большинстве из интере­сующих нас задач влияние значений зависимой переменной в точках, со­седних с некоторой узловой, на зна­чение в этой узловой точке обуслов­лено процессами конвекции и диффу­зии. Следовательно, увеличение зна­чения в одной узловой точке должно, при прочих равных условиях, привести к увеличению (а не уменьшению) зна­чения в соседней узловой точке. Тогда,

как видно из уравнения (2.13), из увеличения  при увеличении  следует, что коэффициенты  и  должны иметь одинаковый знак. Другими словами, в общем случае, описываемом уравне­нием (2.15), знаки коэффициентов перед значениями зависимой переменной в соседних точках  и коэффициента перед ее зна­чением в центральной точке  должны быть одинаковыми. Можно, конечно, выбрать их так, чтобы они все были положительными или отрицательными. Договоримся записывать разностный аналог с положительными коэффициентами. Тогда правило можно сфор­мулировать следующим образом: все коэффициенты ( и ) всегда должны быть положительными.

Комментарии. Из определения коэффициентов (2.14) видно, что иллюстрация   дискретизации   уравнения   теплопроводности действительно удовлетворяет правилу положительности коэффициентов. Однако, имеются многочисленные аппроксимации, в которых данное правило часто нарушается. Обычно следствием этого является физически не­правдоподобное решение. Наличие отрицательного «соседнего» коэффициента может привести к ситуации, в которой увеличение температуры на границе вызывает уменьшение температуры в ближайшей узловой точке.

Отрицательность коэффициента при линеаризации источникового члена. Из определений коэффициентов (2.18) вид­но, что коэффициент  может стать отрицательным за счет . Этого можно полностью избежать, потребовав, чтобы  не был положительным. Сформулируем теперь правило в следующем виде: при линеаризации источникового члена в виде  коэффициент  всегда должен быть отрицателен или равен нулю.

Замечания. Правило не настолько произвольно, как оно зву­чит. На самом деле для большинства физических процессов угол наклона касательной к кривой, описывающей источниковый член как функцию зависимой переменной, отрицателен. Действительно, если бы  был положительным, физический процесс мог бы стать неустойчивым. Положительность  свидетельствует о росте источникового члена при увеличении , а это, в свою очередь, может привести, если нет эффективного механизма отвода теп­лоты, к возрастанию  и т. д. С вычислительной точки зрения во избежание неустойчивостей и физически нереальных решений целе­сообразно сохранять  отрицательным. Следует отметить, что принцип отрицательности  существен для счета.

Сумма соседних коэффициентов. Часто в рассмат­риваемое уравнение входят только производные зависимой пере­менной. При этом функции  и  ( — зависимая переменная данного уравнения,  — произвольная постоянная) удовлетворяют дифференциальному уравнению. Это свойство дифференциального уравнения также должно отразиться в его дискретном аналоге. Следовательно, уравнение (2.15) должно быть удовлетворено и в случае, если  и все  увеличить на постоянную. Из этого требования следует равенство  сумме соседних коэффициентов. Таким образом, правило можно сформулировать в виде: для случаев, когда дифференциальное уравнение удовлетворяется так­же при добавлении к зависимой переменной постоянной величины, необходимо, чтобы

.	(2.19)

Обсуждение. Легко видеть, что уравнение (2.13) действительно удовлетворяет этому правилу. Оно означает, что значение в сред­ней точке  является средневзвешенным значений в соседних точ­ках . В отличие от коэффициентов в (2.13) коэффициенты уравнения (2.17) не подчиняются данному правилу. Однако для этого случая правило неприменимо. Если источниковый член зави­сит от , то сумма  не удовлетворяет дифференциальному уравнению. Однако даже в этих случаях правило не следует забывать, так как его можно применять при рассмотрении част­ного случая уравнения. Если, например, положить в (2.17) , правило можно применить и оно действительно выполняется.

Если дифференциальному уравнению удовлетворяют как , так и , искомое температурное поле не становится неоднознач­ным или неопределенным. Значения  можно сделать определен­ными с помощью соответствующих граничных условий. Выполнение правила гарантирует, что, например, при увеличении темпера­туры границы на постоянное значение все температуры увеличатся точно на это же значение.

Можно взглянуть на правило с другой стороны: при отсут­ствии источника и равенстве температур в соседних точках тем­пература в центре  должна иметь такое же значение. В этих условиях только плохая аппроксимация не дает .